栈及栈的应用

| 分类于

前言

前面提到过函数栈帧，是编译器用来实现函数调用的一种数据结构。这种数据结构有其独特的特性，在解决某些问题时使用栈的方式会轻巧很多.在这里我们自己实现一个栈并用此栈来实现一个简单迷宫，解决括号匹配问题

栈的初步了解

1.什么是栈

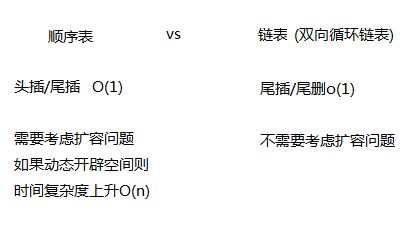
栈就是一种线性的数据结构，他只能在一端进行插入或者进行删除，操作受限。其中允许进行插入或者删除的一端叫做栈顶。栈的插入和删除我们称为入栈，出栈。栈的顺序存储结构叫做顺序栈，链式结构叫做链栈。两种线性结构都可以构成一个栈，且两者都有各自的优缺点。稍做对比

这样比较看来链栈的优点似乎更多一点，在入栈出栈问题上两种数据结构时间复杂度都相同，但链栈他不用考虑扩容问题。但是老师教过我们一个写代码的隐藏原则：KYS(keep you simple) 即一个程序如果能用多种方式实现我们还是优先使用写起来更为简单的那一种。与链表相比用顺序表来写一个栈就简单一些，所以最终我们选择顺序栈

2.栈的特点

先进后出，后进先出。就像是一排走进死胡同的汽车，第一个进去的车只能等前面的车依次走完后他才能最后一个出来。

2.顺序栈的实现

栈的定义

实际上就是一个顺序表，用数组来模拟栈，用top来记录数组中的元素个数，同时他也作为栈顶，因为每多一个元素top就会加一

1
2
3
4
5
6
7
8
typedef int SDatatype;
#define MAX_SIZE 100

typedef struct Stack
{
	SDatatype arr[MAX_SIZE];
	int top;
}Stack;

栈的初始化

即栈中无元素

1
2
3
4
5
//初始化
void StackInit(Stack *ps)
{
	ps->top = 0;
}

栈的销毁

让top为0，即销毁所有元素

1
2
3
4
5
//销毁
void StackDestroy(Stack *ps)
{
	ps->top = 0;
}

入栈操作

入栈操作即尾插

1
2
3
4
5
6
7
//入栈(尾插)
void StackPush(Stack *ps,SDatatype data)
{
	assert(ps->top < MAX_SIZE);
	ps->arr[ps->top] = data;
	ps->top++;
}

出栈操作

出栈即尾删

1
2
3
4
5
6
//出栈(尾删)
void StackPop(Stack *ps)
{
	assert(ps->top > 0);
	ps->top--;
}

查看栈顶元素

即查看数组最后一个元素

1
2
3
4
5
6
//返回栈顶元素
int StackTop(const Stack *ps)
{
	assert(ps->top > 0);
	return ps->arr[ps->top - 1];
}

查看栈大小

即查看数字元素个数

1
2
3
4
5
//返回栈大小（栈里的元素个数）
int StackSize(Stack *ps)
{
	return ps->top;
}

判断栈是否为空,为空返回1，否则返回0

1
2
3
4
int StackEmpty(Stack *ps)
{
	return ps->top == 0 ? 1 : 0;
}

这样便建立好了一个顺序栈，我们可以对他进行想要的操作。整体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

typedef int SDatatype;
#define MAX_SIZE 100

typedef struct Stack
{
	SDatatype arr[MAX_SIZE];
	int top;
}Stack;

//初始化
void StackInit(Stack *ps)
{
	ps->top = 0;
}

//销毁
void StackDestroy(Stack *ps)
{
	ps->top = 0;
}

//入栈(尾插)
void StackPush(Stack *ps,SDatatype data)
{
	assert(ps->top < MAX_SIZE);
	ps->arr[ps->top] = data;
	ps->top++;
}

//出栈(尾删)
void StackPop(Stack *ps)
{
	assert(ps->top > 0);
	ps->top--;
}

//返回栈顶元素
int StackTop(const Stack *ps)
{
	assert(ps->top > 0);
	return ps->arr[ps->top - 1];
}

//返回栈大小（栈里的元素个数）
int StackSize(Stack *ps)
{
	return ps->top;
}

//判断栈是否为空，为空返回1，不为空返回0
int StackEmpty(Stack *ps)
{
	return ps->top == 0 ? 1 : 0;
}

三个栈的应用试题

1.括号匹配问题

题目要求：给出一段类型不唯一的字符串，判断其中的每一种括号是否匹配、例：

1
2
3
4
char a[] = "(())abc{[(])}"; // 左右括号次序匹配不正确
char b[] = "(()))abc{[]}"; // 右括号多于左括号
char c[] = "(()()abc{[]}"; // 左括号多于右括号
char d[] = "(())abc{[]()}";//括号匹配

解题思路：
遍历数组：
如果遇到左括号：进行入栈操作
如果遇到右括号：①判断栈内是否有元素
如果栈为空：则右括号多；
如果栈不为空：比较当前栈顶元素是否和当前右括号匹配
匹配：出栈，继续比较下一个
不匹配：左右括号不匹配
如果是其他字符：不做栈的操作
当遍历完所有元素栈内还有元素则说明左括号多，没有元素了说明括号匹配

具体代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
//括号匹配代码部分
#include"Stack2.h"

void MatchBrackets(const char *str)
{
	Stack stack;
	StackInit(&stack);

	const char *p = str;
	while (*p != '\0')
	{
		switch (*p)
		{
		case'(':
		case'{':
		case'[':
			StackPush(&stack, *p);
			break;
		case')':
		case'}':
		case']':
			if (StackEmpty(&stack))
			{
				printf("右括号多\n");
				return;
			}
			else
			{
				if ((*p == ')'&&StackTop(&stack) == '(' ||
					*p == '}'&&StackTop(&stack) == '{' ||
					*p == ']'&&StackTop(&stack) == '['))
				{
					StackPop(&stack);
				}
				else
				{
					printf("左右括号不匹配\n");
					return;
				}
			}
		default:
			break;
		}
		p++;

	}
	if (StackEmpty(&stack) == 1)
	{
		printf("匹配\n");
	}

	else{
		printf("左括号多\n");
	}
}


void Test()
{
	char a[] = "(())abc{[(])}"; // 左右括号次序匹配不正确
	char b[] = "(()))abc{[]}"; // 右括号多于左括号
	char c[] = "(()()abc{[]}"; // 左括号多于右括号
	char d[] = "(())abc{[]()}";

	MatchBrackets(a);
	MatchBrackets(b);
	MatchBrackets(c);
	MatchBrackets(d);
}

int main()
{
	Test();
	system("pause");
	return 0;
}

2.迷宫问题

整体思路：用一个二维数组建立一个迷宫，1代表可走的路，2代表墙体，即不能走的地方，创建一个栈用来保存迷宫坐标。从入口点开始走起，遵从左上右下的方式走迷宫，每走一步就将走过的路（坐标）压入栈中，并标记为2，如果走着发现没有路可走了且还没有找到出口，则开始回溯，将走过的路依次出栈，出一个便重新判断一次他的左上右下是否能走，若能走再次压入栈中，直到找到出口为止。

栈的定义

与上一题不同，迷宫栈的定义中他的数据类型也需要我们重新定义，因为这个栈中压入的元素是一个坐标。所以我们需要自定义一个坐标类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#define MAX_SIZE 100

 typedef struct
{
	int x;
	int y;
}Position;

typedef Position SDatatype;   

typedef struct
{
	Position arr[MAX_SIZE];
	int top;
 }

迷宫的创建

此处创建一个简单迷宫（只有一个出口，切通路间不带环）。我们用一个二维数组来表示迷宫，0代表墙，是不能走的地方，1代表路

1
2
3
4
5
6
7
8
9
10
11
#define ROWS 6
#define COLS 6

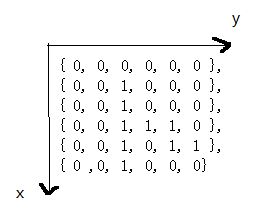
int Maze[ROWS][COLS] = {
	{ 0, 0, 0, 0, 0, 0 },
	{ 0, 0, 1, 0, 0, 0 },
	{ 0, 0, 1, 0, 0, 0 },
	{ 0, 0, 1, 1, 1, 0 },
	{ 0, 0, 1, 0, 1, 1 },
	{ 0, 0, 1, 0, 0, 0 }
};

在这里要注意迷宫的坐标问题。上方为y轴，左边为x轴,如图：

走迷宫代码具体分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
void PrintMaze()
{
	for (int i = 0; i < ROWS; i++)
	{
		for (int j = 0; j < COLS; j++)
		{
			if (Maze[i][j] == 1)
			{
				printf(" ");
			}
			else if (Maze[i][j] == 0)
			{
				printf("#");                      //这里的墙和走过的路的标记字符都可以换
			}
			else if (Maze[i][j] == 2)
			{
				printf("*");
			}
			else
			{
				printf("过");
			}
		}
		printf("\n");
	}
}

void GoMaze()
{
    //创建一个栈并把它初始化
	Stack stack;
	StackInit(&stack);
	//定义好迷宫的入口
	Position entry = { 5, 2 };
	Position pos = entry;
	
	while (1)
	{
		//将入口标记为走过的位置
		Maze[pos.x][pos.y] = 2;
	
		//将入口压栈
		StackPush(&stack, pos);

		//判断左边是否能走
		if (Maze[pos.x][pos.y-1] == 1)
		{
			pos.y = pos.y - 1;
			StackPush(&stack, pos);
			Maze[pos.x][pos.y] = 2;

			if ((pos.x == 0 || pos.x == 5 || pos.y == 0 || pos.y == 5))
			{
				printf("找到出口\n");
				PrintMaze();
				return;
			}
		}

		//判断上边是否能走
		else if (Maze[pos.x - 1][pos.y] == 1)
		{
			pos.x = pos.x - 1;
			StackPush(&stack, pos);
			Maze[pos.x][pos.y] = 2;

			if ((pos.x == 0 || pos.x == 5 || pos.y == 0 || pos.y == 5))
			{
				printf("找到出口\n");
				PrintMaze();
				return;
			}
		}

		//判断右边是否能走
		else if (Maze[pos.x][pos.y + 1] == 1)
		{
			pos.y = pos.y + 1;
			StackPush(&stack, pos);
			Maze[pos.x][pos.y] = 2;

			if ((pos.x == 0 || pos.x == 5 || pos.y == 0 || pos.y == 5))
			{
				printf("找到出口\n");
				PrintMaze();
				return;
			}
		}

		//判断下边是否能走
		else if (Maze[pos.x + 1][pos.y] == 1)
		{
			pos.x = pos.x + 1;
			StackPush(&stack, pos);
			Maze[pos.x][pos.y] = 2;


			if ((pos.x == 0 || pos.x == 5 || pos.y == 0 || pos.y == 5))
			{
				printf("找到出口\n");
				PrintMaze();
				return;

			}
		}

		//如果上下左右都不能走则进行回溯，找到前一个坐标再次进行判断，若还是不能走则依次回溯进行前一个坐标的判断
		else
		{
			pos = StackTop(&stack);
			//Maze[pos.x][pos.y] = 1;
			StackPop(&stack);
			if (StackEmpty(&stack)) {
				printf("结束\n");
				return;
			}
			pos = StackTop(&stack);
			StackPop(&stack);
		}

		system("cls");
		PrintMaze(Maze);
		Sleep(300);

	}
}

运行结果